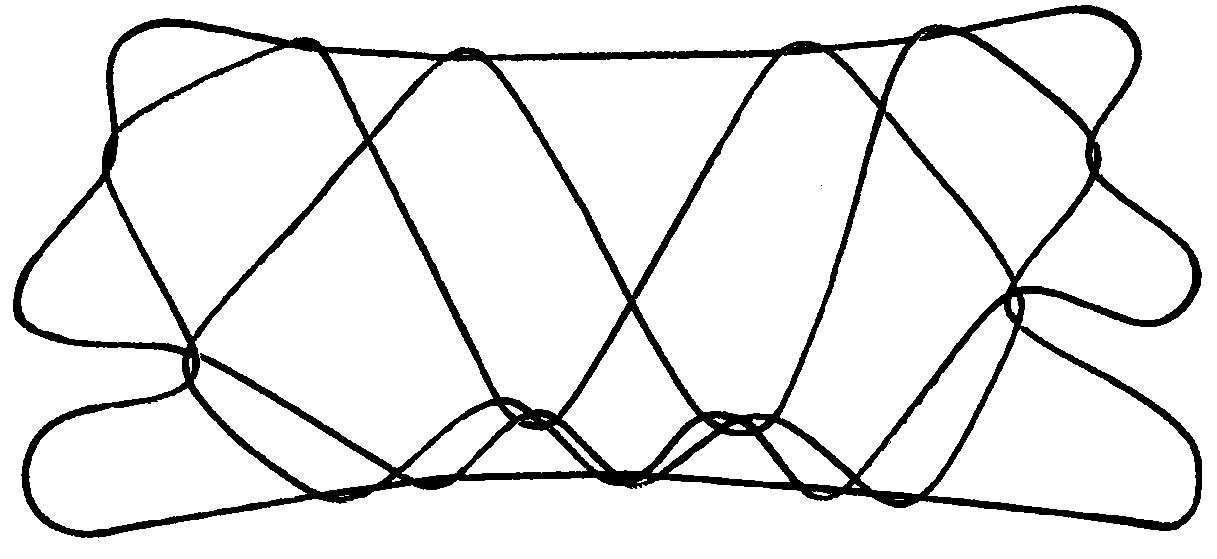
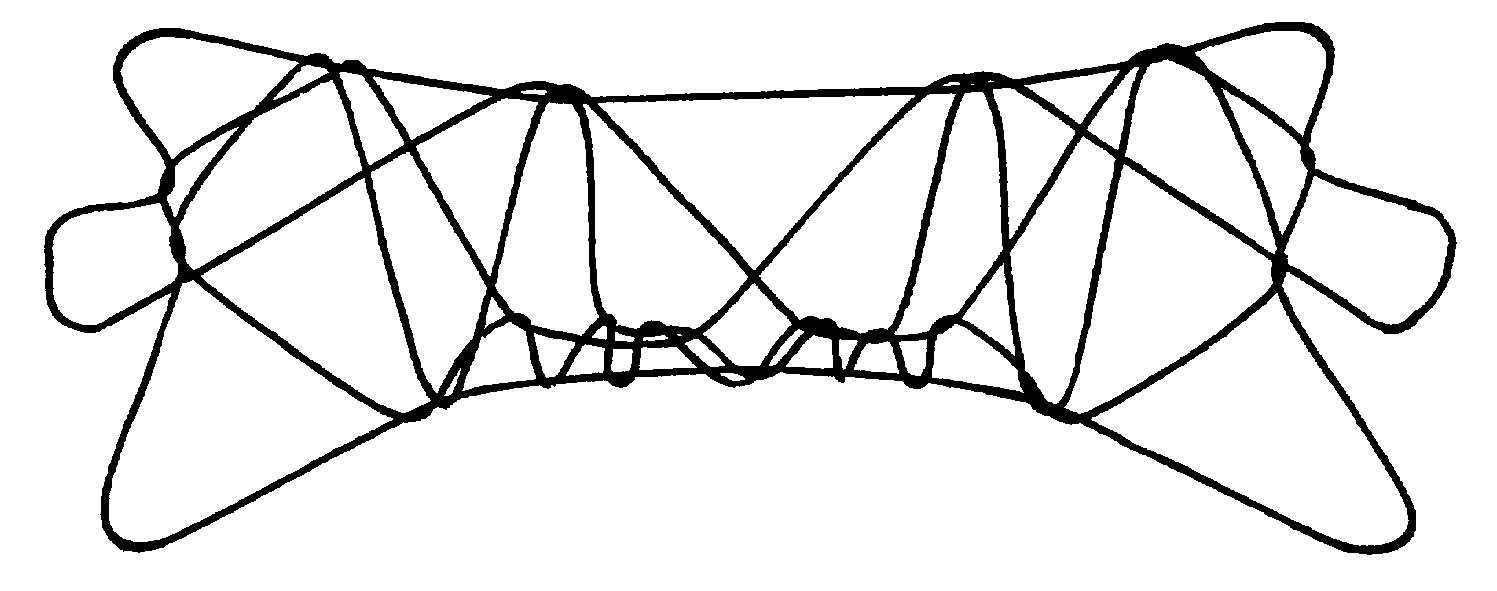
the first five universes

Once the students have mastered the ten basic weaves and can use each of them with some facility, I teach them how to alter the path the thumbs take before retrieving one of the little finger strings during the first or second weave.

First, I review how the parent figure is made (set up loom, do an a weave, reset the loom, do another a weave, and extend), and remind them that the shorthand notation for this sequence is a a.

Then I ask “What would happen if during the first weave you passed each thumb up through the lower index loop (i.e., over the far lower index string) before retrieving the near little finger string and completing the a weave?” The result would be a new figure! In fact, one can envision doing any of the ten simple weaves a-e’ after first passing the thumb up through the lower index loop, which means that ten new figures are easily created.

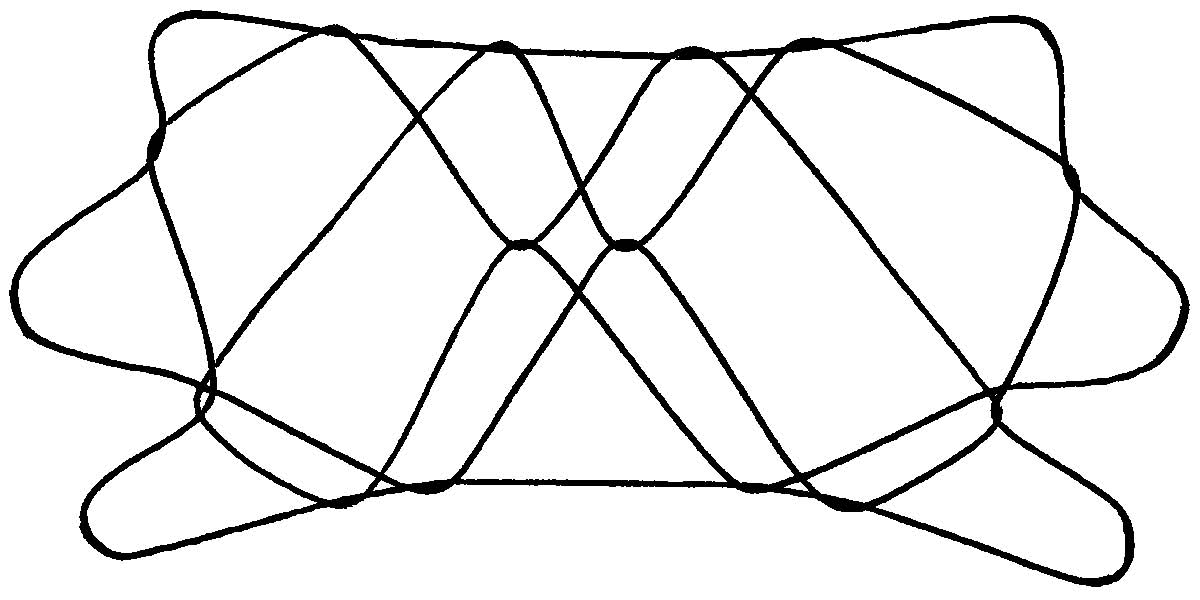
In other words, by altering the thumb’s pathway during the initial part of the weave, you enter a “parallel universe” populated by another entire set of figures equal in size to the original set. For this reason, I refer to this set of weaves as “A-Universe weaves” and use an uppercase A to indicate that the thumb should pass over the far lower index string before doing any of the ten simple weaves. The result of weaving Aa followed by a (Aa a)is shown below.

The ten non-simple weaves in the A-Universe series are written as:

Aa, Ab, Ac, Ad, Ae, Aa’, Ab’, Ac’, Ad’, Ae’

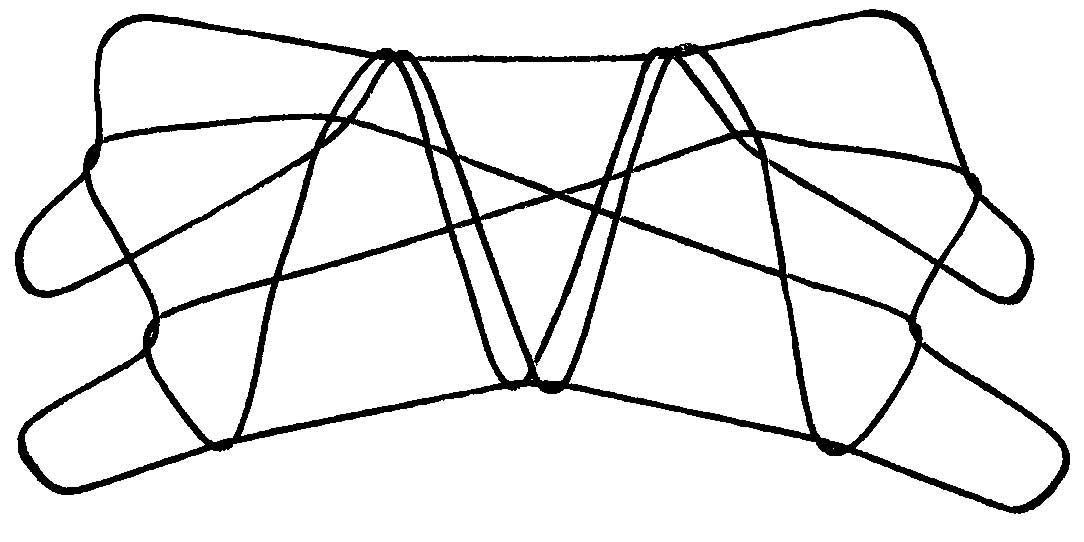
One can also imagine passing each thumb down through the lower index loop (i.e., over the lower near index string) before doing any of the ten simple weaves. Again, the result would be ten more unique figures (Ba a below).

The ten non-simple weaves in the B-Universe are written as:

Ba, Bb, Bc, Bd, Be, Ba’, Bb’, Bc’, Bd’, Be’

If one simply passes the thumb over both lower index strings before retrieving a little finger string, one has entered the C-Universe whose weaves are written as:

Ca, Cb, Cc, Cd, Ce, Ca’, Cb’, Cc’, Cd’, Ce’

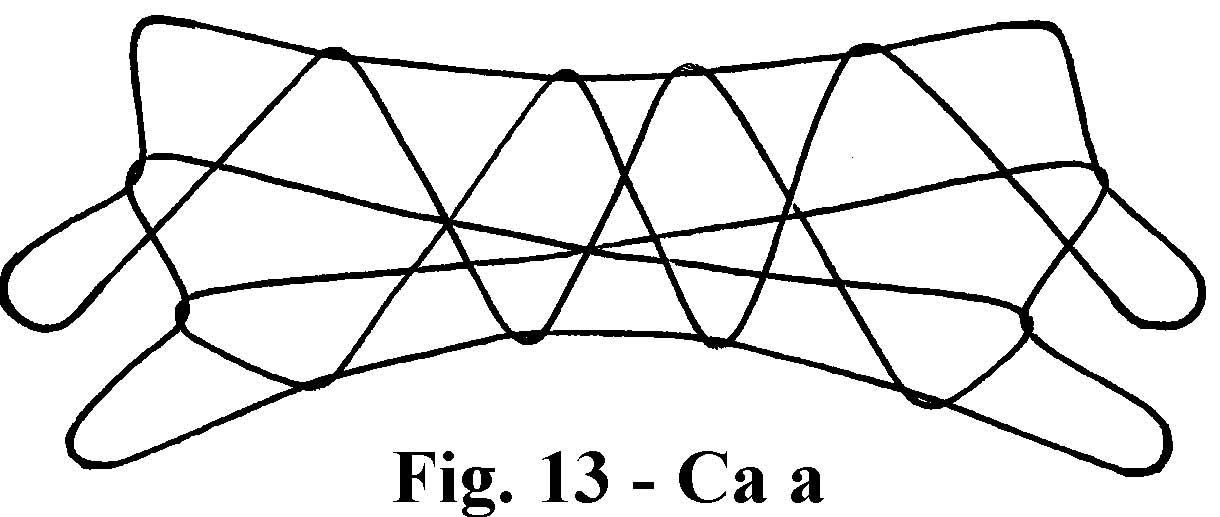
See figure below for the result of weaving Ca a.

an extended discussion of the A, B and C universes

Now let’s increase the complexity a bit: First pass each thumb under the lower near index string, pick up the lower far index string and return. Now pass each thumb over the lower near index string (pushing it down) and retrieve one of the little finger strings (i.e., do one of the ten simple weaves, a-e’). As you return you will need to draw the retrieved string through the “hole” (i.e., the space between the intertwined lower near index and lower far index strings). Note the two-weave pattern Da a below.

This set of weaves is D-Universe:

Da, Db, Dc, Dd, De, Da’, Db’, Dc’, Dd’, De’

In a D-Universe weave, you make the lower far index string go under then over the lower near index string (analogous to a simple d weave in which you make the near little finger string go under then over the far little finger string). Can you guess how to do an E-Universe weave? — make the lower far index string go over then under the lower near index string. Here’s how it’s done: Pass each thumb over the lower near index string and pick up the lower far index string, gently withdraw the thumb and reinsert it in the opposite direction (use the tip of your middle finger to temporarily hold the loop during the reinsertion), then retrieve one of the little finger strings (i.e., do one of the ten simple weaves,). As you return you will need to draw the retrieved string through the “hole” (i.e., the space between the intertwined lower near index and lower far index strings).

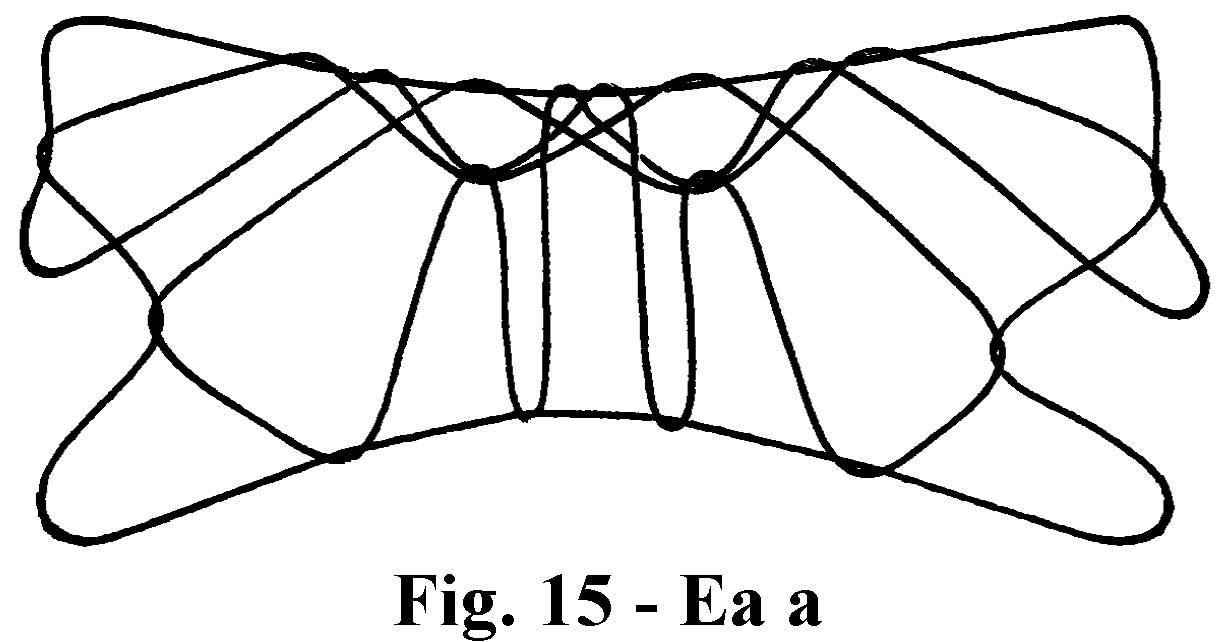
Below you’ll find the result of weaving Ea a.

This set of weaves is E-Universe:

Ea, Eb, Ec, Ed, Ee, Ea’, Eb’, Ec’, Ed’, Ee’

an extended discussion of the D and E universes

What this means is twofold. First you now have fifty more weaves (ten in each Universe) with which to weave different patterns. That is mindboggling enough when you think that with the sixty weaves we can now form:

60 squared or 3,600 two weave patterns

60 cubed or 216,000 three weave patterns

It would take several semesters to make this many figures during class time alone

weaves Aa and Aa’ from the viewpoint of the maker

an extended discussion of the 10 men system seen from the viewpoint of the maker

extended discussion of the first five universes

things to consider

Try forming the three-weave figure a a a on your hands. You should notice that the last two a’s merely add small loops to the lower frame string. You should then conclude that any further a’s will only add more loops.

But now form a Aa’ a on your hands and you should notice that there is a richness introduced into the figure by blocking the “collapse” of the two inverse weaves (a a’) with an A-Universe move.

This is, in fact, why i invented the Universe moves — i tried to see what an “almost collapse” of the figure would achieve, and i was pleasantly surprised.

In summary, Universe moves are useful for (1) blocking reciprocal weaves; and (2) pulling the web back up onto the top frame string in cases where the design has collapsed.

This could best be shown by forming the following two figures (a rather long string is required):

a Aa’ a a

a Aa’ a Bc a

You should be surprised at the result. The Bc weave is a crucial one in some of the higher order figures I form in the Ten Men series.

But don’t be deterred from experimenting and finding your own special weaves among the Universes. i haven’t begun to scratch the surface of having tried them all. I’ve merely imagined the large number of possible differences I can try. The final word on Ten Men figures will probably never be written!